Manufacturer’s Catalogues
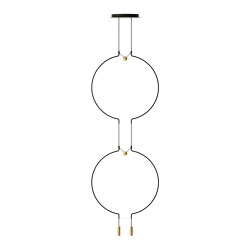
Euler PL GMP
Ceiling lights from Axolight, Designed by Cambi, Scatena, Turini
Product description
More about this product
Manufacturer
Axolight
Family
Architonic ID
1259059
Order number
PLEULGMP
Year of Launch
2014
More products from Axolight
Downloads
Contact information
Address
1410 Broadway, Ste 2104, 10018 New York United States
This product has been discontinued.
More products from Axolight

More from
AxolightContact information
Address
1410 Broadway, Ste 2104, 10018 New York United States